Lois de Kirchhoff en Électricité

Introduction

Les lois de Kirchhoff constituent un ensemble de deux principes fondamentaux en électricité, formulés par le physicien allemand Gustav Kirchhoff en 1845. Ces lois sont essentielles pour analyser et comprendre les circuits électriques complexes, permettant de déterminer les courants, tensions et résistances dans des réseaux de circuits comportant plusieurs boucles et nœuds. Grâce à ces lois, les ingénieurs et scientifiques peuvent résoudre des problèmes électriques qui ne peuvent pas être abordés par les simples lois d’Ohm.

Objectifs de l’article

Cet article explore en profondeur les lois de Kirchhoff, en expliquant non seulement leurs fondements théoriques, mais également leurs applications pratiques dans différents contextes de l’électronique et de l’électricité. Les objectifs spécifiques incluent :

Comprendre les principes sous-jacents des lois de Kirchhoff.
Apprendre à utiliser les lois de Kirchhoff pour analyser des circuits électriques complexes.
Explorer des exemples pratiques illustrant l’importance des lois dans des systèmes électriques modernes.

Importance des Lois de Kirchhoff

Les lois de Kirchhoff sont à la base de l’analyse des circuits électriques en courant continu (CC) et alternatif (CA). Elles sont largement utilisées dans de nombreuses disciplines, allant de l’électronique grand public aux systèmes industriels et de communication. Ces lois permettent de simplifier l’analyse de circuits en réseaux, même ceux comportant des éléments non linéaires tels que des transistors ou des diodes.

Les Lois de Kirchhoff

La Loi des Nœuds (Loi des Courants)

La première des lois de Kirchhoff est appelée loi des courants ou loi des nœuds. Elle se base sur le principe de conservation de la charge électrique, stipulant que :

« La somme algébrique des courants entrant dans un nœud est égale à la somme des courants qui en sortent. »

En d’autres termes, pour un point donné dans un circuit où plusieurs conducteurs se rejoignent (appelé nœud), le courant total qui y entre doit être égal au courant total qui en sort. Cela découle du fait que la charge électrique ne peut ni s’accumuler ni disparaître dans un nœud ; elle doit se conserver.

Formulation Mathématique

Si un nœud est connecté à plusieurs branches avec des courants $I_1, I_2, \dots, I_n$ , la loi des nœuds peut être écrite sous la forme :

$\sum I_{\text{entrée}} = \sum I_{\text{sortie}}$

En convention, les courants entrants dans le nœud sont pris comme positifs, et les courants sortants comme négatifs. Cela se traduit mathématiquement par :

$\sum I = 0$

Ceci est un principe clé pour l’analyse des circuits, car il permet de réduire le nombre d’inconnues et facilite le calcul des courants dans des circuits complexes.

Exemples Pratiques

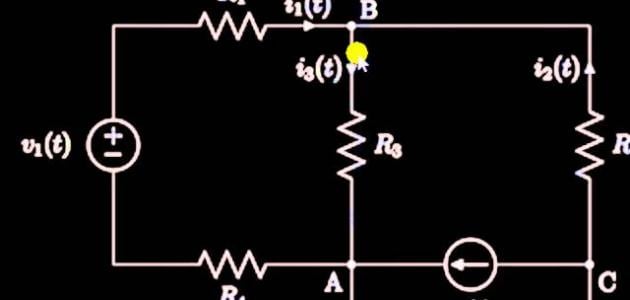
La loi des nœuds est particulièrement utile dans les circuits comportant plusieurs branches ou composants, tels que les circuits en parallèle. Par exemple, dans un circuit avec un nœud connecté à trois résistances, si les courants traversant ces résistances sont respectivement $I_1$ , $I_2$ , et $I_3$ , la loi des courants s’appliquera pour calculer les intensités dans chaque branche.

La Loi des Mailles (Loi des Tensions)

La seconde loi de Kirchhoff est la loi des tensions ou loi des mailles. Cette loi repose sur le principe de conservation de l’énergie et stipule que :

« La somme des tensions le long d’une maille fermée est égale à zéro. »

En d’autres termes, dans un circuit fermé (appelé maille), l’énergie totale fournie par les sources de tension (telles que des batteries ou des générateurs) doit être égale à l’énergie consommée par les charges résistives ou autres éléments du circuit.

Formulation Mathématique

La loi des tensions s’écrit :

$\sum V = 0$

où $V$ représente la tension aux bornes de chaque élément de la maille. Les tensions fournies par les sources d’alimentation sont prises avec un signe positif, tandis que les chutes de tension aux bornes des résistances ou autres composants passifs sont prises avec un signe négatif.

Exemple avec une Maille Simple

Considérons un circuit en série avec une source de tension $V$ , une résistance $R_1$ , et une autre résistance $R_2$ . La loi des mailles de Kirchhoff peut être appliquée comme suit :

$V – V_{R1} – V_{R2} = 0$

où $V_{R1}$ et $V_{R2}$ représentent les chutes de tension aux bornes des résistances $R_1$ et $R_2$ , respectivement. Si l’on connaît les valeurs de $R_1$ et $R_2$ , ainsi que la tension $V$ , cette équation permet de déterminer les courants dans chaque élément du circuit.

Applications des Lois de Kirchhoff

Analyse de Circuits Complexes

Les lois de Kirchhoff sont indispensables dans l’analyse de circuits comportant plusieurs nœuds et mailles. Dans des systèmes électriques et électroniques modernes, il est souvent nécessaire de comprendre comment la tension et le courant se répartissent dans un réseau de composants connectés de manière complexe.

Exemples d’Applications

Circuits en Pont de Wheatstone : Ces circuits sont utilisés pour mesurer des résistances inconnues avec une grande précision. Les lois de Kirchhoff permettent de résoudre les tensions et courants dans chaque branche.
Analyse des Circuits RLC : Dans les circuits comprenant des résistances (R), des inductances (L), et des condensateurs (C), les lois de Kirchhoff permettent de déterminer le comportement du circuit en fonction de la fréquence du signal d’entrée.
Circuits Électroniques : Les circuits intégrés modernes, tels que ceux utilisés dans les ordinateurs et les smartphones, reposent sur une analyse détaillée des tensions et des courants, qui est rendue possible par les lois de Kirchhoff.

Utilisation dans l’Électronique de Puissance

Dans les applications de l’électronique de puissance, telles que les alimentations électriques, les convertisseurs et les onduleurs, les lois de Kirchhoff permettent d’assurer que les courants et les tensions sont distribués de manière efficace et sûre à travers le système.

Avantages et Limites des Lois de Kirchhoff

Avantages

Simplicité et Universalité : Les lois de Kirchhoff sont simples et peuvent être appliquées à tout type de circuit électrique, indépendamment de sa complexité.
Analyse Précise des Réseaux Complexes : Elles permettent de résoudre des systèmes de circuits comportant plusieurs composants actifs et passifs, en fournissant des outils puissants pour analyser les réseaux multi-boucles.
Utilisation dans les Simulations : Les logiciels de simulation de circuits, tels que SPICE, utilisent les lois de Kirchhoff pour modéliser le comportement des circuits en conditions réelles.

Limites

Hypothèses Simplificatrices : Les lois de Kirchhoff reposent sur des hypothèses telles que l’absence de champs magnétiques variables. Dans les circuits où ces effets sont significatifs, des méthodes plus avancées comme l’électromagnétisme doivent être utilisées.
Applications aux Circuits Non Linéaires : Dans les circuits comportant des composants non linéaires (comme des diodes ou des transistors), l’application des lois de Kirchhoff devient plus complexe, car les tensions et les courants ne suivent pas des relations linéaires.

Table: Comparaison des Lois de Kirchhoff avec d’autres Principes en Électricité

Principe	Description	Domaine d’application	Avantages	Inconvénients
Loi des Nœuds	Somme des courants dans un nœud égale à zéro	Circuits multi-branches	Simple à appliquer	Nécessite la connaissance des courants
Loi des Mailles	Somme des tensions dans une maille égale à zéro	Circuits en boucle fermée	Indispensable pour les boucles	Difficulté avec des sources non linéaires
Loi d’Ohm	Relation entre tension, courant, et résistance	Circuits linéaires simples	Très courante dans les circuits CC	Ne s’applique pas aux circuits CA complexes
Théorème de Thévenin	Simplification d’un réseau à une seule source	Circuits complexes	Facilite l’analyse de grands réseaux	Nécessite des calculs préliminaires
Théorème de Norton	Réduction d’un circuit complexe à un courant	Circuits complexes	Simplifie les calculs pour les courants	Nécessite des calculs complexes

Conclusion

Les lois de Kirchhoff représentent une avancée fondamentale dans la compréhension et l’analyse des circuits électriques. Elles fournissent un cadre indispensable pour résoudre des systèmes complexes comportant plusieurs nœuds et boucles, et elles sont largement utilisées dans des domaines tels que l’électronique de puissance, les télécommunications, et les systèmes informatiques. Bien que ces lois soient basées sur des hypothèses simplificatrices, elles restent une des pierres angulaires de l’électrotechnique moderne. Leur maîtrise est essentielle pour tout ingénieur ou technicien travaillant avec des systèmes électriques, et elles continueront à jouer un rôle central dans les innovations futures en électricité et en électronique.

Plus d’informations

Le loi de Kirchhoff est un ensemble de principes fondamentaux en électrotechnique et en ingénierie électrique, nommé d’après le physicien allemand Gustav Kirchhoff. Ces lois sont essentielles pour comprendre le comportement des circuits électriques, qu’ils soient en courant continu (DC) ou en courant alternatif (AC). Les deux lois principales de Kirchhoff sont la loi des nœuds et la loi des mailles. Ces lois permettent de résoudre les équations de circuit et d’analyser les réseaux électriques complexes.

1. La Loi des Nœuds (ou Loi de Kirchhoff des Courants)

La loi des nœuds stipule que la somme des courants entrant dans un nœud (ou jonction) d’un circuit électrique est égale à la somme des courants sortants de ce nœud. En d’autres termes, la somme algébrique des courants à un nœud est toujours nulle. Cette loi repose sur le principe de la conservation de la charge électrique.

Matériellement, cela peut être exprimé par l’équation suivante :

$\sum_{k=1}^n I_k = 0$

où $I_k$ représente le courant à l’entrée ou à la sortie du nœud. Cette loi est également connue sous le nom de première loi de Kirchhoff.

Exemples Pratiques

Circuit Simple :
Si un nœud reçoit des courants de 2 A et 3 A, et envoie un courant de 5 A, la loi des nœuds stipule que la somme des courants entrants (2 A + 3 A) doit être égale à la somme des courants sortants (5 A).
Analyse de Circuits Complexes :
Dans des circuits plus complexes avec plusieurs nœuds, cette loi est utilisée pour écrire des équations pour chaque nœud, ce qui permet de déterminer les courants dans différentes branches du circuit.

2. La Loi des Mailles (ou Loi de Kirchhoff des Tensions)

La loi des mailles stipule que la somme algébrique des tensions dans une maille (ou boucle fermée) d’un circuit électrique est égale à zéro. Cela découle du principe de conservation de l’énergie, signifiant que l’énergie fournie par les sources de tension est égale à l’énergie dissipée dans les éléments résistifs de la maille.

Matériellement, cela peut être exprimé par l’équation suivante :

$\sum_{k=1}^n V_k = 0$

où $V_k$ représente la tension à travers chaque élément de la maille. Cette loi est également connue sous le nom de deuxième loi de Kirchhoff.

Exemples Pratiques

Circuit avec Une Source de Tension et Deux Résistances :
Considérons une maille avec une source de tension $V$ et deux résistances $R_1$ et $R_2$ . La loi des mailles stipule que la tension fournie par la source doit être égale à la somme des tensions aux bornes des résistances :

$V – (I \cdot R_1) – (I \cdot R_2) = 0$

où $I$ est le courant circulant dans la maille.
Analyse des Circuits AC :
Pour les circuits en courant alternatif, la loi des mailles est utilisée de la même manière, mais les tensions et courants sont représentés par des nombres complexes (impédances) pour tenir compte des effets de la réactance inductive et capacitive.

Application des Lois de Kirchhoff

Les lois de Kirchhoff sont utilisées dans une variété d’applications, allant de la conception de circuits électroniques à l’analyse des réseaux électriques complexes. Voici quelques domaines où ces lois sont particulièrement utiles :

Conception de Circuits Électroniques :
Les ingénieurs utilisent les lois de Kirchhoff pour concevoir des circuits qui respectent des critères spécifiques de performance, comme la gestion de la tension et du courant dans les circuits de puissance ou les circuits analogiques.
Analyse des Réseaux Électriques :
Dans les réseaux électriques de grande envergure, les lois de Kirchhoff aident à calculer les courants et les tensions dans différents points du réseau, facilitant la gestion et l’optimisation des systèmes de distribution d’électricité.
Études de Consommation Énergétique :
Les lois de Kirchhoff sont essentielles pour comprendre comment l’énergie est consommée dans les appareils électriques et pour concevoir des systèmes qui minimisent les pertes d’énergie.

Limites des Lois de Kirchhoff

Bien que les lois de Kirchhoff soient extrêmement utiles, elles ne sont pas sans limites. Elles supposent que les circuits sont idéaux, sans perte d’énergie due à des effets non idéaux comme les pertes par effet Joule ou les interférences électromagnétiques. De plus, elles sont appliquées dans le cadre des circuits linéaires et peuvent ne pas s’appliquer directement à des circuits non linéaires ou à haute fréquence sans ajustements appropriés.

En résumé, les lois de Kirchhoff jouent un rôle crucial dans l’analyse et la conception des circuits électriques. La loi des nœuds permet de comprendre comment les courants se distribuent à travers les différents composants d’un circuit, tandis que la loi des mailles aide à analyser les tensions et à s’assurer que l’énergie est conservée dans une boucle fermée. Ces principes sont fondamentaux pour les ingénieurs et les techniciens travaillant dans le domaine de l’électrotechnique et de l’électronique, et ils fournissent une base solide pour la résolution des problèmes électriques complexes.