Bien sûr, je serais ravi de vous fournir des exemples d’algorithmes pour résoudre des problèmes simples. Les algorithmes sont essentiellement des séquences d’instructions bien définies conçues pour résoudre un problème spécifique. Voici quelques exemples courants :
-
Tri à bulles :
C’est l’un des algorithmes de tri les plus simples. Il parcourt la liste à plusieurs reprises, compare les éléments adjacents et les échange s’ils sont dans le mauvais ordre. Cela se poursuit jusqu’à ce que la liste entière soit triée.
La solution définitive pour raccourcir les liens et gérer vos campagnes digitales de manière professionnelle.
• Raccourcissement instantané et rapide des liens
• Pages de profil interactives
• Codes QR professionnels
• Analyses détaillées de vos performances digitales
• Et bien plus de fonctionnalités gratuites !
-
Recherche binaire :
Cet algorithme est utilisé pour rechercher un élément dans une liste triée. Il commence par diviser la liste en deux parties égales et détermine dans quelle moitié l’élément cible peut se trouver. Ensuite, il répète le processus dans la moitié appropriée jusqu’à ce que l’élément soit trouvé ou que la liste soit épuisée. -
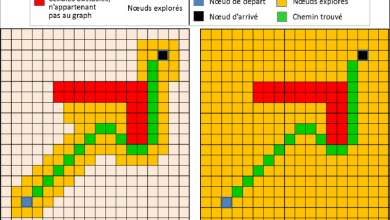
Algorithme de Dijkstra :
Utilisé pour trouver le chemin le plus court entre deux nœuds dans un graphe pondéré, cet algorithme attribue des distances aux nœuds à partir du nœud source et met à jour ces distances en fonction des arêtes adjacentes jusqu’à ce que le nœud cible soit atteint. -
Algorithme de recherche de chaîne de caractères (par exemple, l’algorithme de Knuth-Morris-Pratt) :
Cet algorithme est utilisé pour rechercher efficacement la présence d’un motif dans une chaîne de caractères. Il utilise une table de préfixe pour éviter de revoir des caractères déjà comparés. -
Algorithme de fusion :
Il s’agit d’un algorithme de tri efficace qui divise récursivement la liste en deux moitiés, trie ces moitiés, puis les fusionne pour obtenir une liste triée. -
Algorithme de recherche linéaire :
C’est l’algorithme le plus simple pour rechercher un élément dans une liste non triée. Il parcourt simplement la liste de manière séquentielle et compare chaque élément avec la valeur cible jusqu’à ce qu’il la trouve ou atteigne la fin de la liste. -
Algorithme de l’allocation des tâches (par exemple, l’algorithme de la méthode hongroise) :
Utilisé pour résoudre les problèmes d’affectation, cet algorithme permet d’attribuer de manière optimale un certain nombre de ressources à un certain nombre de tâches, en minimisant ou maximisant un critère donné. -
Algorithme de calcul du plus grand commun diviseur (PGCD) :
Cet algorithme calcule le plus grand commun diviseur de deux nombres en utilisant l’algorithme d’Euclide, qui consiste à répéter la division jusqu’à ce que le reste devienne zéro. -
Algorithme de tri rapide (Quicksort) :
Il s’agit d’un algorithme de tri récursif qui divise la liste en fonction d’un pivot, place les éléments plus petits que le pivot à sa gauche et les éléments plus grands à sa droite, puis trie récursivement les sous-listes gauche et droite. -
Algorithme de recherche d’arbres (par exemple, l’algorithme de parcours en profondeur ou en largeur) :
Utilisé pour parcourir efficacement les arbres et trouver des informations spécifiques, cet algorithme explore les nœuds de l’arbre selon différentes stratégies (profondeur d’abord ou largeur d’abord).
Ces exemples représentent une petite sélection des nombreux algorithmes disponibles pour résoudre une variété de problèmes. Chacun a ses propres avantages, limitations et domaines d’application spécifiques. En combinant ces algorithmes de manière appropriée, il est possible de résoudre des problèmes complexes dans divers domaines informatiques et mathématiques.
Plus de connaissances

Bien sûr, je peux approfondir davantage sur certains des algorithmes mentionnés précédemment, ainsi que vous présenter quelques autres exemples pour enrichir votre compréhension.
-
Tri à bulles :
Le tri à bulles est simple à comprendre mais peu efficace pour des listes de grande taille. Son principe est de parcourir la liste de gauche à droite, en comparant les éléments adjacents et en les échangeant s’ils sont dans le mauvais ordre. Cette opération est répétée jusqu’à ce que la liste soit entièrement triée. Malgré son inefficacité, le tri à bulles est souvent utilisé pour des listes de taille très réduite ou comme exemple pédagogique. -
Recherche binaire :
La recherche binaire est remarquable pour sa rapidité dans la recherche d’éléments dans une liste triée. Elle divise la liste en deux à chaque étape, réduisant ainsi le nombre d’éléments à examiner à chaque itération. Cela en fait un choix efficace pour les grandes quantités de données, car le nombre d’itérations nécessaires est logarithmique par rapport à la taille de la liste. -
Algorithme de Dijkstra :
Connu également sous le nom de plus court chemin, cet algorithme est utilisé dans de nombreux domaines, notamment pour trouver le chemin le plus court dans les réseaux de télécommunications, les réseaux informatiques, ou encore dans la planification de trajets dans les transports. Il fonctionne de manière itérative, en sélectionnant à chaque étape le nœud non visité le plus proche du point de départ, puis en mettant à jour les distances des nœuds adjacents en fonction des chemins les plus courts découverts jusqu’à présent. -
Algorithme de Knuth-Morris-Pratt :
Contrairement à la méthode naïve de recherche de chaîne de caractères, qui consiste à glisser une fenêtre le long de la chaîne principale et à vérifier si une correspondance est trouvée à chaque position, l’algorithme de Knuth-Morris-Pratt utilise une table de préfixe pour sauter les comparaisons inutiles. Cela le rend plus efficace, en particulier pour les chaînes de caractères de grande taille ou pour les recherches répétitives dans de grandes bases de données. -
Algorithme de fusion :
L’algorithme de fusion suit le paradigme de la division et de la conquête. Il divise récursivement la liste en deux moitiés, trie ces moitiés, puis les fusionne pour obtenir une liste triée. Bien que son pire cas soit O(n log n), il est souvent préféré à d’autres algorithmes de tri pour sa stabilité (il conserve l’ordre relatif des éléments égaux) et son efficacité sur les listes liées. -
Algorithme de l’allocation des tâches (méthode hongroise) :
Aussi connu sous le nom de méthode hongroise, cet algorithme est utilisé pour résoudre les problèmes d’affectation dans lesquels il s’agit d’attribuer de manière optimale un certain nombre de ressources à un certain nombre de tâches, tout en minimisant ou maximisant un critère donné (par exemple, le coût total). Il est largement utilisé dans la logistique, la planification de la production, ou encore dans l’optimisation des trajets de véhicules. -
Algorithme de l’algorithme d’Euclide pour le PGCD :
L’algorithme d’Euclide est une méthode efficace pour calculer le plus grand commun diviseur (PGCD) de deux nombres entiers. Il repose sur le principe que le PGCD de deux nombres reste inchangé si on soustrait le plus petit du plus grand jusqu’à ce que les deux nombres soient égaux, puisque le PGCD ne change pas si on soustrait le plus petit du plus grand. -
Algorithme de tri rapide (Quicksort) :
Le tri rapide (Quicksort) est un algorithme de tri récursif basé sur la division et la conquête. Il choisit un élément pivot dans la liste, partitionne la liste en fonction de cet élément, puis trie récursivement les sous-listes à gauche et à droite du pivot. Malgré son pire cas de complexité O(n^2), le tri rapide est souvent rapide en pratique et est largement utilisé. -
Algorithme de recherche d’arbres (parcours en profondeur ou en largeur) :
Les algorithmes de recherche d’arbres sont utilisés pour parcourir efficacement les arbres binaires ou généraux. Le parcours en profondeur explore le plus loin possible le long d’une branche avant de revenir en arrière, tandis que le parcours en largeur explore tous les nœuds d’un niveau avant de passer au niveau suivant. Ces algorithmes sont utilisés dans de nombreux domaines, y compris les langages de programmation pour la manipulation des structures arborescentes.
Ces exemples illustrent la diversité des algorithmes et leurs applications dans différents domaines. Ils représentent une fraction des nombreux algorithmes disponibles pour résoudre des problèmes variés, et chaque algorithme a ses propres avantages, inconvénients et domaines d’application spécifiques.