Guide complet de l’algorithme A*

Introduction

L’algorithme A* est l’un des algorithmes de recherche de chemin les plus populaires et les plus efficaces utilisés en informatique, notamment dans les domaines de l’intelligence artificielle, de la robotique, des jeux vidéo et de la planification. Développé par Peter Hart, Nils Nilsson et Bertram Raphael en 1968, A* combine les avantages de la recherche en largeur et de la recherche en profondeur, tout en utilisant une heuristique pour guider la recherche de manière optimale.

---

Histoire et Contexte

L’algorithme A* a été conçu dans le contexte de la recherche de chemins optimaux dans des graphes, une problématique courante en intelligence artificielle et en robotique. Avant A*, plusieurs algorithmes existaient, tels que la recherche en largeur (BFS) et la recherche en profondeur (DFS), mais ils présentaient des limitations en termes d’efficacité et d’optimalité. A* a été développé pour combiner la rapidité de la BFS avec l’efficacité d’une heuristique, permettant ainsi de trouver des chemins optimaux plus rapidement.

Principes de Base de l’A*

A* est un algorithme de recherche informée qui utilise une fonction d’évaluation pour déterminer l’ordre dans lequel les nœuds doivent être explorés. Il maintient deux listes principales : la liste ouverte (nœuds à explorer) et la liste fermée (nœuds déjà explorés). À chaque étape, A* sélectionne le nœud avec le coût total estimé le plus bas (f(n) = g(n) + h(n)) et explore ses voisins, mettant à jour les coûts et les chemins en conséquence.

Fonctionnement de l’Algorithme A*

États et Noeuds

• État : Représente une configuration particulière dans l’espace de recherche (par exemple, une position sur une grille).
• Nœud : Représente un état avec des informations supplémentaires telles que le coût pour y arriver et l’heuristique estimée jusqu’à l’objectif.

Listes Ouverte et Fermée

• Liste Ouverte : Contient les nœuds qui sont identifiés pour exploration future.
• Liste Fermée : Contient les nœuds qui ont déjà été explorés.

Fonctions de Coût : g(n), h(n), et f(n)

• g(n) : Coût réel pour atteindre le nœud n depuis le nœud de départ.
• h(n) : Heuristique estimant le coût restant pour atteindre l’objectif à partir du nœud n.
• f(n) = g(n) + h(n) : Coût total estimé pour atteindre l’objectif en passant par le nœud n.

Choix de l’Heuristique

L’heuristique est cruciale pour la performance de l’A*. Une bonne heuristique peut réduire considérablement le temps de recherche en guidant l’algorithme vers l’objectif de manière plus efficace.

Propriétés des Heuristiques Admissibles

• Admissible : Une heuristique est admissible si elle ne surestime jamais le coût réel pour atteindre l’objectif. Cela garantit que l’A* trouve toujours le chemin optimal.
• Consistante (ou Monotone) : Une heuristique est consistante si, pour chaque nœud n et chaque successeur n’ de n, h(n) ≤ c(n, n’) + h(n’). La consistance implique l’admissibilité.

Exemples d’Heuristiques

• Distance Euclidienne : Utilisée dans des espaces continus sans obstacles.
• Distance de Manhattan : Utilisée dans des grilles où les mouvements sont limités à des directions orthogonales.
• Distance de Chebyshev : Utilisée lorsque les mouvements diagonaux sont autorisés et ont le même coût que les mouvements orthogonaux.

Pseudocode de l’A*

function A*(start, goal)
    openSet := priority queue containing start
    cameFrom := empty map

    gScore[start] := 0
    fScore[start] := heuristic(start, goal)

    while openSet is not empty
        current := node in openSet with lowest fScore[current]

        if current == goal
            return reconstruct_path(cameFrom, current)

        remove current from openSet
        add current to closedSet

        for each neighbor of current
            if neighbor in closedSet
                continue

            tentative_gScore := gScore[current] + dist(current, neighbor)

            if neighbor not in openSet
                add neighbor to openSet
            else if tentative_gScore >= gScore[neighbor]
                continue

            cameFrom[neighbor] := current
            gScore[neighbor] := tentative_gScore
            fScore[neighbor] := gScore[neighbor] + heuristic(neighbor, goal)

    return failure

Implémentation de l’A*

Structures de Données

• File de Priorité (Open Set) : Utilisée pour sélectionner le nœud avec le plus petit f(n) à chaque itération. Une implémentation efficace peut utiliser un tas binaire.
• Map pour Came From : Stocke le chemin optimal en enregistrant le nœud précédent pour chaque nœud exploré.
• Tables de gScore et fScore : Stockent respectivement les coûts g(n) et f(n) pour chaque nœud.

Optimisations

• Utilisation de Heaps Binaires ou de Fibres Heaps : Pour améliorer les performances des opérations de la file de priorité.
• Mémoïsation des Heuristiques : Calculer les heuristiques une seule fois par nœud et les stocker pour éviter des recalculs répétitifs.
• Élagage des Chemins Non Optimaux : Ignorer les nœuds qui ne peuvent pas conduire à un chemin plus court que celui déjà trouvé.

Applications de l’A*

Recherche de Chemin

L’application la plus courante de l’A* est la recherche de chemin dans des environnements connus, tels que les cartes routières ou les grilles de jeu, permettant de trouver le chemin le plus court ou le plus efficace entre deux points.

Jeux Vidéo

Dans les jeux vidéo, A* est utilisé pour l’intelligence artificielle des personnages non-joueurs (PNJ) afin de naviguer de manière réaliste dans l’environnement du jeu, évitant les obstacles et trouvant des chemins optimaux.

Planification de Mouvements

En robotique, A* aide les robots à planifier leurs mouvements dans des environnements complexes, en tenant compte des obstacles et en optimisant les trajectoires pour l’efficacité énergétique ou le temps.

Avantages et Inconvénients de l’A*

Avantages

• Optimalité : Lorsque l’heuristique est admissible, A* garantit de trouver le chemin optimal.
• Flexibilité : Peut être adapté à divers types de problèmes en modifiant l’heuristique.
• Efficacité : Généralement plus rapide que les algorithmes de recherche non informés comme BFS ou DFS grâce à l’utilisation de l’heuristique.

Inconvénients

• Consommation Mémoire : Peut nécessiter une grande quantité de mémoire pour stocker les listes ouverte et fermée, surtout dans les espaces de recherche vastes.
• Dépendance à l’Heuristique : La performance dépend fortement de la qualité de l’heuristique utilisée.
• Complexité en Temps : Dans le pire des cas, le temps d’exécution peut être exponentiel par rapport à la profondeur de la solution.

Variantes de l’A*

A* avec Mémoire Limitée

Pour pallier les problèmes de consommation mémoire, des variantes comme A* IDA* (Iterative Deepening A*) utilisent une approche de recherche en profondeur itérative, réduisant ainsi l’empreinte mémoire au prix d’une augmentation du temps de calcul.

A* Bidirectionnel

Cette variante exécute deux recherches A* simultanément : une part du départ et l’autre de l’objectif, se rencontrant en milieu de chemin. Cela peut réduire le temps de recherche en divisant le problème en deux parties plus petites.

Exemples Pratiques

Exemple Pas à Pas

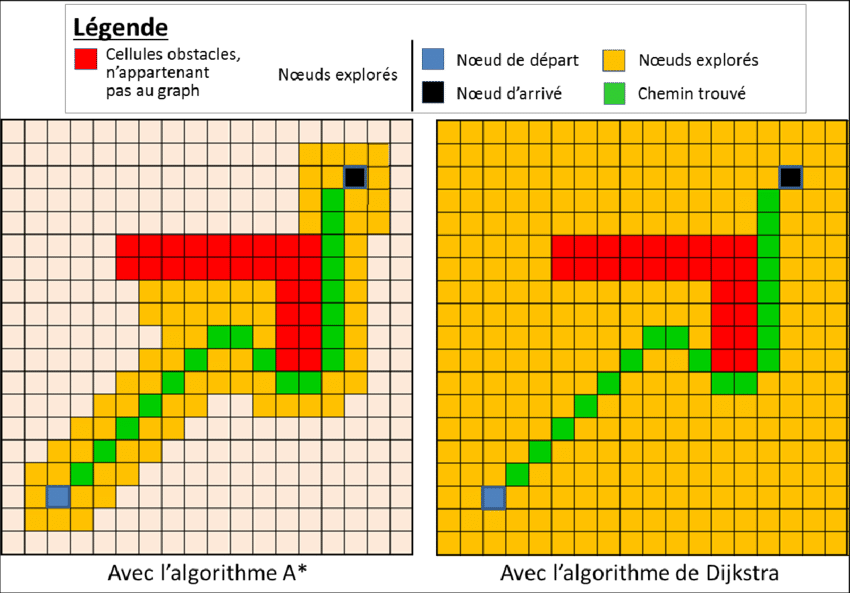
Considérons une grille 5×5 avec un point de départ en (0,0) et un objectif en (4,4). Supposons que certaines cellules sont des obstacles.

1. Initialisation : Ajouter le nœud de départ à la liste ouverte avec g(n)=0 et f(n)=h(n).
2. Itération 1 : Sélectionner (0,0), explorer ses voisins (1,0) et (0,1).
3. Calcul des Scores :
   • Pour (1,0) : g=1, h=heuristique(1,0) = 7 → f=8
   • Pour (0,1) : g=1, h=heuristique(0,1) = 7 → f=8
4. Itération 2 : Sélectionner (1,0), explorer ses voisins, et ainsi de suite jusqu’à atteindre (4,4).

Implémentation en Python

Voici une implémentation simple de l’algorithme A* en Python :

import heapq

def heuristic(a, b):
    return abs(a[0] - b[0]) + abs(a[1] - b[1])  # Distance de Manhattan

def astar(grid, start, goal):
    open_set = []
    heapq.heappush(open_set, (0, start))
    came_from = {}
    g_score = {start: 0}
    f_score = {start: heuristic(start, goal)}
    closed_set = set()

    while open_set:
        current = heapq.heappop(open_set)[1]

        if current == goal:
            # Reconstituer le chemin
            path = []
            while current in came_from:
                path.append(current)
                current = came_from[current]
            path.append(start)
            path.reverse()
            return path

        closed_set.add(current)

        neighbors = get_neighbors(grid, current)
        for neighbor in neighbors:
            if neighbor in closed_set:
                continue

            tentative_g_score = g_score[current] + 1  # Supposons que le coût est 1

            if neighbor not in g_score or tentative_g_score < g_score[neighbor]:
                came_from[neighbor] = current
                g_score[neighbor] = tentative_g_score
                f_score[neighbor] = tentative_g_score + heuristic(neighbor, goal)
                heapq.heappush(open_set, (f_score[neighbor], neighbor))

    return None  # Pas de chemin trouvé

def get_neighbors(grid, node):
    neighbors = []
    x, y = node
    directions = [(-1,0),(1,0),(0,-1),(0,1)]  # Haut, Bas, Gauche, Droite
    for dx, dy in directions:
        nx, ny = x + dx, y + dy
        if 0 <= nx < len(grid) and 0 <= ny < len(grid[0]):
            if grid[nx][ny] == 0:  # 0 représente un espace libre
                neighbors.append((nx, ny))
    return neighbors

# Exemple d'utilisation
grid = [
    [0, 1, 0, 0, 0],
    [0, 1, 0, 1, 0],
    [0, 0, 0, 1, 0],
    [1, 1, 0, 1, 0],
    [0, 0, 0, 0, 0]
]

start = (0, 0)
goal = (4, 4)
path = astar(grid, start, goal)
print("Chemin trouvé :", path)

Explications :

• Heuristique : Utilise la distance de Manhattan, appropriée pour les grilles avec mouvements orthogonaux.
• Grille : Représentée par une liste de listes où 0 est un espace libre et 1 est un obstacle.
• Fonction astar : Implémente l’algorithme A*, en utilisant une file de priorité (heapq) pour la liste ouverte.
• Reconstitution du Chemin : Une fois l’objectif atteint, le chemin est reconstruit en remontant à partir de l’objectif jusqu’au départ.

 

L’algorithme A* est une technique de recherche de chemin très flexible et adaptable, ce qui en fait l’un des algorithmes les plus populaires dans de nombreux domaines. Voici quelques points supplémentaires pour approfondir votre compréhension :

1. Variations de l’algorithme A :* Il existe plusieurs variations de l’algorithme A* qui sont utilisées en fonction des besoins spécifiques de chaque problème. Par exemple, l’A* pondéré (Weighted A*) permet de contrôler l’équilibre entre l’exploration exhaustive et la recherche dirigée par l’heuristique en utilisant un paramètre de poids. D’autres variations incluent l’A* bidirectionnel, qui explore simultanément à partir du nœud de départ et du nœud d’arrivée pour accélérer la recherche dans certains cas.
2. Complexité et optimisation : Bien que l’algorithme A* soit efficace pour de nombreux problèmes, sa complexité peut devenir un défi dans des environnements où le nombre de nœuds est très élevé. Dans de tels cas, des techniques d’optimisation telles que la mémorisation des nœuds explorés (caching) ou l’utilisation de structures de données efficaces comme les tas binomiaux ou les tas de Fibonacci peuvent être utilisées pour améliorer les performances.
3. Applications pratiques : L’algorithme A* est largement utilisé dans de nombreuses applications pratiques. Dans les jeux vidéo, il est utilisé pour la planification de trajectoires des personnages non joueurs (PNJ) ou des unités contrôlées par l’ordinateur. Dans les systèmes de navigation GPS, il est utilisé pour calculer les itinéraires les plus courts entre les points de départ et d’arrivée. Dans le domaine de la robotique, il est utilisé pour la planification de mouvement des robots autonomes.
4. Connaissances du domaine : L’efficacité de l’algorithme A* dépend souvent de la qualité de la fonction heuristique utilisée pour estimer le coût restant jusqu’au nœud d’arrivée. Dans certains cas, il peut être nécessaire de personnaliser la fonction heuristique en fonction des connaissances spécifiques du domaine. Par exemple, dans un environnement de grille où les mouvements sont restreints à des directions discrètes, une heuristique basée sur la distance de Manhattan peut être plus appropriée.
5. Limitations : Bien que l’algorithme A* soit capable de trouver des chemins optimaux dans de nombreux cas, il peut rencontrer des difficultés dans des environnements très dynamiques ou avec des coûts de mouvement variables. Dans de tels cas, des techniques de replanification en temps réel ou d’autres algorithmes de recherche de chemin plus adaptés peuvent être nécessaires.

En résumé, l’algorithme A* est une technique puissante et polyvalente de recherche de chemin qui trouve des applications dans de nombreux domaines. Sa capacité à trouver des solutions optimales et sa flexibilité en font un outil précieux pour la résolution de problèmes de planification de trajectoire dans divers contextes. Cependant, comme pour tout algorithme, il est important de comprendre ses forces et ses limitations pour l’appliquer de manière efficace dans des scénarios réels.

Conclusion

L’algorithme A* est un outil puissant pour la recherche de chemins optimaux dans divers contextes. Sa capacité à combiner une recherche exhaustive avec des heuristiques informées le rend à la fois flexible et efficace. Bien que son principal inconvénient soit la consommation potentiellement élevée de mémoire, plusieurs variantes et optimisations permettent de surmonter ces limitations dans des applications pratiques. Maîtriser A* ouvre la porte à de nombreuses applications en intelligence artificielle, robotique et au-delà.