Le passage entre le système décimal et le système binaire constitue un élément fondamental dans le domaine de l’informatique et des sciences de l’informatique. Cette conversion entre deux bases numériques distinctes revêt une importance particulière dans la compréhension du fonctionnement interne des ordinateurs, des circuits électroniques et des algorithmes liés au traitement de l’information.
Le système décimal, également connu sous le nom de système décimal de position, est basé sur la valeur dix. Chaque chiffre dans ce système représente une puissance de dix. Ainsi, les chiffres sont 0, 1, 2, 3, 4, 5, 6, 7, 8 et 9. La position d’un chiffre dans un nombre indique la puissance de dix correspondante. Par exemple, dans le nombre 365, le chiffre 5 est à la position des unités (10^0), le chiffre 6 est à la position des dizaines (10^1), et le chiffre 3 est à la position des centaines (10^2).
La solution définitive pour raccourcir les liens et gérer vos campagnes digitales de manière professionnelle.
• Raccourcissement instantané et rapide des liens
• Pages de profil interactives
• Codes QR professionnels
• Analyses détaillées de vos performances digitales
• Et bien plus de fonctionnalités gratuites !
D’un autre côté, le système binaire est le fondement de la représentation de l’information dans les ordinateurs. Contrairement au système décimal, le système binaire utilise uniquement deux chiffres, 0 et 1, pour représenter toutes les valeurs. Chaque chiffre dans le système binaire est une puissance de deux. Ainsi, les positions dans un nombre binaire sont des puissances successives de deux. Par exemple, dans le nombre binaire 1101, le chiffre 1 est à la position des unités (2^0), le chiffre 0 est à la position des deux (2^1), le chiffre 1 est à la position des quatre (2^2), et le chiffre 1 est à la position des huit (2^3).
La conversion du système décimal au système binaire implique de décomposer le nombre décimal en une somme de puissances de deux, en utilisant les chiffres binaires appropriés pour représenter chaque puissance. Pour ce faire, on divise le nombre décimal par 2 de manière répétée, en enregistrant les restes à chaque étape. Le résultat final est obtenu en lisant les restes de bas en haut.
Prenons un exemple concret pour illustrer le processus. Convertissons le nombre décimal 25 en binaire. On divise 25 par 2, on obtient 12 avec un reste de 1. En divisant à nouveau 12 par 2, on obtient 6 avec un reste de 0. En poursuivant ce processus, on trouve que 6 divisé par 2 donne 3 avec un reste de 0, et 3 divisé par 2 donne 1 avec un reste de 1. Enfin, 1 divisé par 2 donne 0 avec un reste de 1. En lisant les restes de bas en haut, on obtient 11001, ce qui est la représentation binaire de 25.
À l’inverse, pour convertir un nombre binaire en décimal, on multiplie chaque chiffre binaire par la puissance de deux correspondante à sa position, puis on additionne ces produits. Par exemple, pour convertir le nombre binaire 11001 en décimal, on calcule 1 * 2^4 + 1 * 2^3 + 0 * 2^2 + 0 * 2^1 + 1 * 2^0, ce qui donne 16 + 8 + 0 + 0 + 1, soit 25, le nombre décimal que nous avions converti précédemment.
Il est essentiel de noter que la conversion entre le système décimal et le système binaire s’étend au-delà des simples nombres entiers. Elle s’applique également aux nombres fractionnaires. La partie entière d’un nombre décimal est convertie de la même manière que les nombres entiers, tandis que la partie fractionnaire est convertie en multipliant les chiffres binaires par les puissances négatives de deux.
Cette transition entre les systèmes numériques joue un rôle crucial dans la programmation informatique, où les instructions et les données sont souvent exprimées en langage binaire. Comprendre cette conversion facilite la compréhension des opérations de base telles que l’addition, la soustraction, la multiplication et la division dans le contexte binaire, ce qui est essentiel pour les développeurs de logiciels et les ingénieurs en informatique.
En résumé, la conversion entre le système décimal et le système binaire constitue un aspect fondamental de l’informatique moderne. Elle offre un aperçu des bases du traitement de l’information dans les ordinateurs, mettant en lumière la manière dont les données sont représentées et manipulées au niveau le plus élémentaire. Cette compréhension est cruciale pour ceux qui souhaitent s’aventurer dans le domaine de l’informatique, que ce soit pour la programmation, la conception de circuits électroniques ou d’autres domaines connexes.
Plus de connaissances
Au-delà de la simple conversion entre le système décimal et le système binaire, il est essentiel de comprendre les applications pratiques de cette transition dans le contexte plus large de l’informatique et des sciences de l’information. La représentation binaire des données revêt une importance significative dans le stockage, la transmission et le traitement de l’information au sein des systèmes informatiques.
L’un des domaines clés où cette conversion est omniprésente est le stockage de l’information dans les mémoires des ordinateurs. Les unités de stockage, telles que les disques durs et les mémoires RAM, utilisent des configurations binaires pour représenter les données. Chaque bit dans la mémoire, la plus petite unité d’information, peut avoir la valeur 0 ou 1. Par conséquent, la conversion entre les systèmes décimal et binaire est essentielle pour comprendre la manière dont les informations sont stockées de manière binaire dans ces dispositifs.
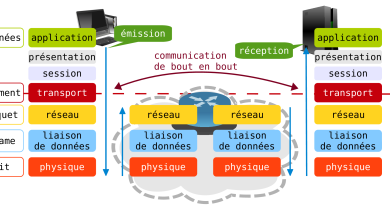
En ce qui concerne la transmission de l’information, notamment à travers les réseaux informatiques, la représentation binaire est également prédominante. Les protocoles de communication, tels que le protocole TCP/IP qui est à la base d’Internet, utilisent des séquences binaires pour transmettre des données entre les dispositifs connectés. Comprendre la conversion entre le système décimal et le système binaire est donc essentiel pour les professionnels des réseaux informatiques qui doivent analyser et interpréter les paquets de données transitant à travers les réseaux.
L’informatique contemporaine repose largement sur la représentation binaire des instructions des processeurs. Les unités centrales de traitement (CPU) des ordinateurs exécutent des opérations arithmétiques et logiques sur des données binaires. Les programmes informatiques, écrits dans des langages de haut niveau tels que C, Python ou Java, sont traduits en langage machine binaire compréhensible par le processeur. La conversion entre les systèmes numériques est donc incontournable pour les programmeurs qui souhaitent comprendre la manière dont leurs codes sont interprétés et exécutés par le matériel informatique.
De plus, dans le domaine de la conception de circuits électroniques, la conversion entre le système décimal et le système binaire est cruciale. Les ingénieurs en électronique utilisent des systèmes binaires pour concevoir des circuits numériques, tels que des processeurs, des mémoires et des unités de traitement graphique. La compréhension de la représentation binaire est essentielle pour concevoir des systèmes électroniques performants et efficaces.
En ce qui concerne les langages de programmation, certains aspects liés à la manipulation directe des bits dans le langage binaire peuvent être abordés dans des langages de bas niveau tels que l’assembleur. Bien que l’utilisation quotidienne de ces langages soit limitée, ils jouent un rôle crucial dans la compréhension du fonctionnement interne des processeurs et dans l’optimisation de la performance des programmes.
Par ailleurs, la conversion entre les systèmes numériques est également liée à la cryptographie, un domaine qui s’attache à sécuriser les communications en ligne et à protéger les données sensibles. Les algorithmes cryptographiques utilisent des opérations sur les nombres binaires pour garantir la confidentialité et l’intégrité des données. Ainsi, la maîtrise de la conversion entre le système décimal et le système binaire est un atout précieux pour ceux impliqués dans la conception et l’analyse de systèmes de sécurité informatique.
En conclusion, la conversion entre le système décimal et le système binaire transcende la simple manipulation de chiffres. Elle constitue une pierre angulaire de l’informatique moderne, influençant divers aspects tels que le stockage des données, la transmission de l’information, la programmation, la conception de circuits électroniques et la sécurité informatique. Comprendre cette transition offre une perspective approfondie sur le fonctionnement interne des ordinateurs, des réseaux informatiques et des technologies émergentes, renforçant ainsi la base de connaissances des professionnels et des passionnés de l’informatique.
