Algorithmes d’analyse arborescente

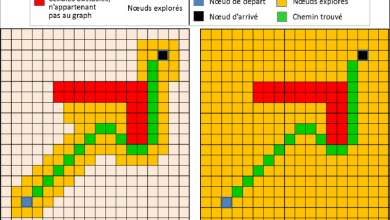
Les algorithmes d’analyse des chemins dans les arbres sont un domaine passionnant de l’informatique qui trouve de nombreuses applications dans divers domaines tels que l’informatique théorique, l’intelligence artificielle, les réseaux informatiques, la bioinformatique et bien d’autres. Ces algorithmes sont conçus pour analyser et manipuler les structures arborescentes, qui sont des structures de données fondamentales largement utilisées pour représenter des relations hiérarchiques.

L’un des problèmes classiques dans ce domaine est celui de trouver des chemins spécifiques ou de calculer diverses mesures de chemins dans un arbre, tels que la longueur du chemin le plus court, le nombre total de chemins possibles, les chemins qui satisfont à certaines conditions données, et bien plus encore. Voici quelques-uns des algorithmes couramment utilisés pour résoudre ces problèmes :

La solution définitive pour raccourcir les liens et gérer vos campagnes digitales de manière professionnelle.

• Raccourcissement instantané et rapide des liens

• Pages de profil interactives

• Codes QR professionnels

• Analyses détaillées de vos performances digitales

• Et bien plus de fonctionnalités gratuites !

Commencez dès maintenant et profitez du service !

1. Parcours en profondeur (Depth-First Search, DFS) :
   DFS est un algorithme fondamental utilisé pour explorer et traverser les arbres en profondeur. En utilisant une approche récursive ou une pile, DFS parcourt aussi loin que possible le long d’une branche de l’arbre avant de faire marche arrière et d’explorer d’autres branches.

2. Parcours en largeur (Breadth-First Search, BFS) :
   BFS est un autre algorithme de parcours d’arbre qui explore l’arbre niveau par niveau. Il commence par le nœud racine, puis explore tous les nœuds adjacents au même niveau avant de passer au niveau suivant.

3. Algorithme de Dijkstra :
   Cet algorithme est utilisé pour trouver le chemin le plus court entre deux nœuds dans un graphe pondéré. Bien qu’il soit généralement utilisé pour les graphes, il peut également être adapté pour les arbres en considérant chaque arête comme ayant un poids égal à 1.

4. Algorithme de Bellman-Ford :
   Similaire à l’algorithme de Dijkstra, Bellman-Ford trouve également le plus court chemin entre deux nœuds dans un graphe pondéré, mais il peut gérer des graphes contenant des arêtes de poids négatif (tant qu’il n’y a pas de cycle de poids négatif).

5. Algorithme de Kruskal :
   Kruskal est utilisé pour trouver un arbre de recouvrement de coût minimum dans un graphe pondéré non orienté. Cet arbre de recouvrement est également connu sous le nom d’arbre couvrant minimal.

6. Algorithme de Prim :
   Similaire à l’algorithme de Kruskal, Prim trouve également un arbre de recouvrement de coût minimum, mais il commence par un seul nœud et développe l’arbre jusqu’à ce qu’il couvre tous les nœuds du graphe.

7. Algorithme de recherche A (A-Star)* :
   Utilisé dans le domaine de l’intelligence artificielle, l’algorithme A* est une méthode de recherche de chemin qui trouve le chemin le plus court entre un nœud initial et un nœud objectif dans un graphe pondéré.

8. Algorithme de recherche en profondeur limitée (Limited Depth-First Search, LDFS) :
   Une variante de DFS où la profondeur de recherche est limitée. Cela peut être utile dans certaines situations où une recherche complète en profondeur n’est pas nécessaire.

Ces algorithmes ne sont que quelques exemples parmi de nombreux autres qui sont utilisés pour l’analyse des chemins dans les arbres. Chaque algorithme a ses propres caractéristiques, avantages et inconvénients, et le choix de l’algorithme dépend souvent de la nature spécifique du problème à résoudre et des contraintes auxquelles il est confronté. En combinant ces algorithmes de manière créative et en les adaptant aux exigences spécifiques, il est possible de résoudre une grande variété de problèmes liés à l’analyse des chemins dans les arbres, contribuant ainsi au développement de solutions efficaces dans de nombreux domaines d’application.

Bien sûr, plongeons un peu plus profondément dans chacun de ces algorithmes et explorons leurs fonctionnalités, leurs applications et leurs performances.

1. Parcours en profondeur (Depth-First Search, DFS) :

   • Fonctionnement : DFS explore aussi loin que possible le long d’une branche avant de revenir en arrière. Cela peut être implémenté de manière récursive ou en utilisant une pile.
   • Applications : Utilisé pour trouver des composantes connexes, des cycles, des chemins entre deux nœuds, et pour d’autres problèmes de recherche ou d’exploration d’arbres et de graphes.
   • Complexité temporelle : O(V + E), où V est le nombre de sommets et E est le nombre d’arêtes.

2. Parcours en largeur (Breadth-First Search, BFS) :

   • Fonctionnement : BFS explore tous les nœuds adjacents d’un même niveau avant de passer au niveau suivant.
   • Applications : Trouver le plus court chemin dans un graphe non pondéré, la recherche de la solution optimale dans les jeux à deux joueurs avec un arbre de jeu, etc.
   • Complexité temporelle : O(V + E), où V est le nombre de sommets et E est le nombre d’arêtes.

3. Algorithme de Dijkstra :

   • Fonctionnement : Trouve le chemin le plus court entre un nœud source et tous les autres nœuds dans un graphe pondéré et orienté.
   • Applications : Routage de réseau, GPS, systèmes de navigation, optimisation de la logistique, etc.
   • Complexité temporelle : O((V + E) log V) avec une implémentation de tas binaire, où V est le nombre de sommets et E est le nombre d’arêtes.

4. Algorithme de Bellman-Ford :

   • Fonctionnement : Trouve le chemin le plus court entre un nœud source et tous les autres nœuds, même dans des graphes contenant des arêtes de poids négatif, tant qu’il n’y a pas de cycle de poids négatif.
   • Applications : Routage de réseau, détection de cycles de coût négatif, planification de projet, etc.
   • Complexité temporelle : O(VE), où V est le nombre de sommets et E est le nombre d’arêtes.

5. Algorithme de Kruskal :

   • Fonctionnement : Construit un arbre de recouvrement minimal en choisissant à chaque étape l’arête de poids minimum qui ne forme pas de cycle.
   • Applications : Réseaux de télécommunications, conception de réseaux électriques, clustering, etc.
   • Complexité temporelle : O(E log E) ou O(E log V), selon l’implémentation utilisée, où E est le nombre d’arêtes et V est le nombre de sommets.

6. Algorithme de Prim :

   • Fonctionnement : Construit un arbre de recouvrement minimal en ajoutant à chaque étape le nœud adjacent le plus proche de l’arbre en construction.
   • Applications : Réseaux de communication, analyse de réseaux routiers, clustering, etc.
   • Complexité temporelle : O(V^2) avec une implémentation naïve, mais peut être améliorée à O(E log V) avec des structures de données appropriées.

7. Algorithme de recherche A (A-Star)* :

   • Fonctionnement : Utilise une fonction heuristique pour guider la recherche de chemin vers le nœud objectif, en minimisant le coût total estimé du chemin.
   • Applications : Planification de trajets, jeux, robotique, etc.
   • Complexité temporelle : Dépend de la fonction heuristique utilisée et de la structure du graphe.

8. Algorithme de recherche en profondeur limitée (Limited Depth-First Search, LDFS) :

   • Fonctionnement : Une variante de DFS où la profondeur de recherche est limitée par une valeur prédéfinie.
   • Applications : Recherche de solutions dans des arbres de jeu avec une profondeur limitée, exploration de grands arbres avec une limite de mémoire, etc.
   • Complexité temporelle : Dépend de la profondeur limite spécifiée.

En combinant ces algorithmes avec d’autres techniques d’optimisation et de conception d’algorithmes, il est possible de résoudre une multitude de problèmes complexes liés à l’analyse des chemins dans les arbres. La sélection de l’algorithme approprié dépendra souvent des caractéristiques spécifiques du problème à résoudre, telles que la structure du graphe, la présence de contraintes particulières, les performances requises, et d’autres considérations pertinentes.